
Quadrilaterals are plane shapes with four sides and four interior angles. (iii) The exterior angle is equal to the sum of the opposite interior angles.

(ii) Two interior angles of a triangle are equal to the opposite exterior angle. (i) The three interior angles of a triangle add up to 180 °. The angles at the bases of the equal sides are equal in size.Įquilateral triangles have three equal sides and three equal angles (each being 60 °).Īcute-angled triangles have three angles each 90 °. Isosceles triangles have two sides of equal length. Scalene triangles have no sides of equal length and no angles that are of equal sizes.

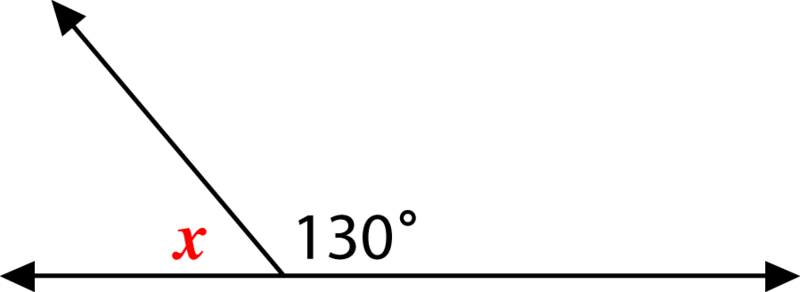
(ii) Triangles are classified according to the lengths of their sides and the sizes of their angles (or both). (i) A triangle is a plane shape with three sides and three angles. Co interior angles are supplementary (together they add up to 180 °"). When two parallel lines are cut by a transversal two pairs of co-interior angles are formed. Alternate angles are equal to each other. When two parallel lines are cut by a transversal two pairs of alternate angles are formed. Corresponding angles are equal to each other. When two parallel lines are cut by a transversal four pairs of corresponding angles are formed. These angles form pairs that are related to each other in specific ways. When two parallel lines are cut by a third line (the transversal) eight angles are formed. (iii) The adjacent angle pairs in vertically opposite angles form pairs of supplementary angles because they are also angles on a straight line. (b) Vertically opposite angles are equal in size. (a) When two lines intersect, two pairs of vertically opposite angles are formed. (c) For supplementary angles, if one angle is x º, the other must be 180 ° - x ° and vice versa. (b) When the sum of two angles is 180 ° those two angles are supplementary angles. (a) Angles on a straight line add up to 180 °. (b) For complementary angles, if one angle is x °, the other must be 90 ° - x ° and vice versa. (a) Angles in a right angle add up to 90 °. You need to choose the correct one when you measure an angle. Angle sizes are measured in degrees ( ° ) from 0 to 360 using a protractor. (i) The size of an angle is the amount of turn from one arm of the angle to the other. Obtuse angles measure more than 90 degrees.Ī straight angle is an angle, whose vertex point has a value of 180 degrees.Īn angle greater than 180 ° and less than 360 °.Ī revolution is a complete turn an angle of exactly 360 °. The property of being perpendicular (perpendicularity) is the relationship between two lines that meet at a right angle ( 90 degrees).Īcute angles measure less than 90 degrees. Angles are measured in degrees, using a protractor. Parallel means two lines that never intersect.Īn angle can be defined as the figure formed by two rays meeting at a common endpoint. It is often described as the shortest distance between any two points. A point represents position only it has zero sizes (that is, zero length, zero width, and zero height).Ī line can be defined as a straight one- dimensional figure that has no thickness and extends endlessly in both directions. It is represented by a dot and named by a capital letter. Terms Used to Talk about Lines and Angles: TermĪ point is the most fundamental object in geometry. Therefore, the two supplementary angles are 108° and 72°.1. Let the two supplementary angles be 3x and 2x,Ī pair of angles are said to be supplementary if the sum of the angles is equal to 180°. Hence, the measure of the required angle is 90°.Įxample: Two supplementary angles are in the ratio of 3: 2.Find the angles. We know, two angles are said to be supplementary if the sum of their measure is equal to 180° ∠AOB and ∠POQ are said to be supplements of each other.Įxample: Find the angle which equals to its supplement ∴ ∠AOB and ∠POQ are supplementary angles. Hence, ∠PQS and ∠SQR are supplementary angles and ∠PQS and ∠SQR are said to be supplements of each other.Įxample: The following ∠AOB and ∠POQ are supplementary angles or not? In the above figure, we see that the sum of two angles is 180° Hence, we can say that they are supplementary angles or supplements of each other. The measure of two angles 120° and 60° are given and when we add up that angles we get 180°. The two angles formed by the hands of the above clock are supplementary. Two angles are said to be supplementary if the sum of their measure is equal to 180°.


 0 kommentar(er)
0 kommentar(er)
